Bigraph

Bigraph#

A bipartite graph (bigraph [1]) is defined as

(1)#\[(V_P+ V_Q, E_bi)\]

where there is no adjacency (i.e., connection) between nodes in either residue set V_P or V_Q. A global residue-residue connection (GlobRRC, see here) is formed by an element from set V_P and an element from set V_Q.

seqNetRR contains a few types of bipartite graphs, that is, patch, memconp, cross, and unchanged. You can also customize a bigraph.

This, we will go through how to define and make a bigraph in Python.

Patch#

The first bigraph we want to show is patch, which is defined by a square centering around a residue pair in a correlation matrix (e.g., residue contact map) as shown in the plot below. We use the patch function below to generate a patch with a length L.

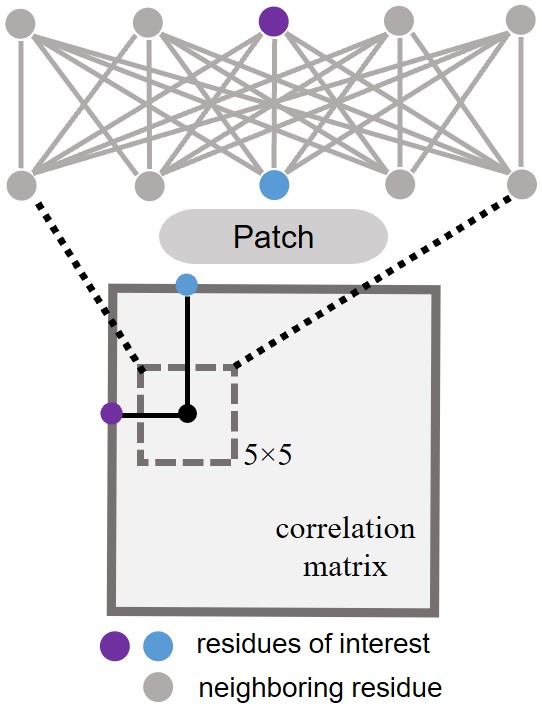
../../../_images/patch.jpg

Caption: Patch bipartite graph in a residue contact map.#

def patch(length, step=1):
    arr = []
    for i in range(-length, length + 1, step):
        for j in range(-length, length + 1, step):
            arr.append([i, j])
    return arr

If we have two residues 1 and 2, how does the TMKit program know them and their neighbouring residues? In fact, either is marked by the coordinate 0. If a neighbouring residue appears on the left side of residue 1, the coordinate of the neighbouring residue is -1 (which will be paired to residue 2), and a neighbouring residue appear on the right side of residue 1 the coordinate of the neighbouring residue is 1 (which will be paired to residue 2).

In TMKit, we use the function below to generate a bigraph of one residue of a residue pair of interest.

Then, we will have the following output, after calling this function by patch(length=5, step=1) where length means the length of one edge of the patch and step means in which step we will skip the positions to the next one.

[[-2, -2], [-2, -1], [-2, 0], [-2, 1], [-2, 2],
 [-1, -2], [-1, -1], [-1, 0], [-1, 1], [-1, 2],
 [0, -2], [0, -1], [0, 0], [0, 1], [0, 2],
 [1, -2], [1, -1], [1, 0], [1, 1], [1, 2],
 [2, -2], [2, -1], [2, 0], [2, 1], [2, 2]]

MemConP#

The second bigraph we show here is memconp, which is used to study the two residues from two different helices that face each other, for example, residue 1 and residue 2 in the plot below.

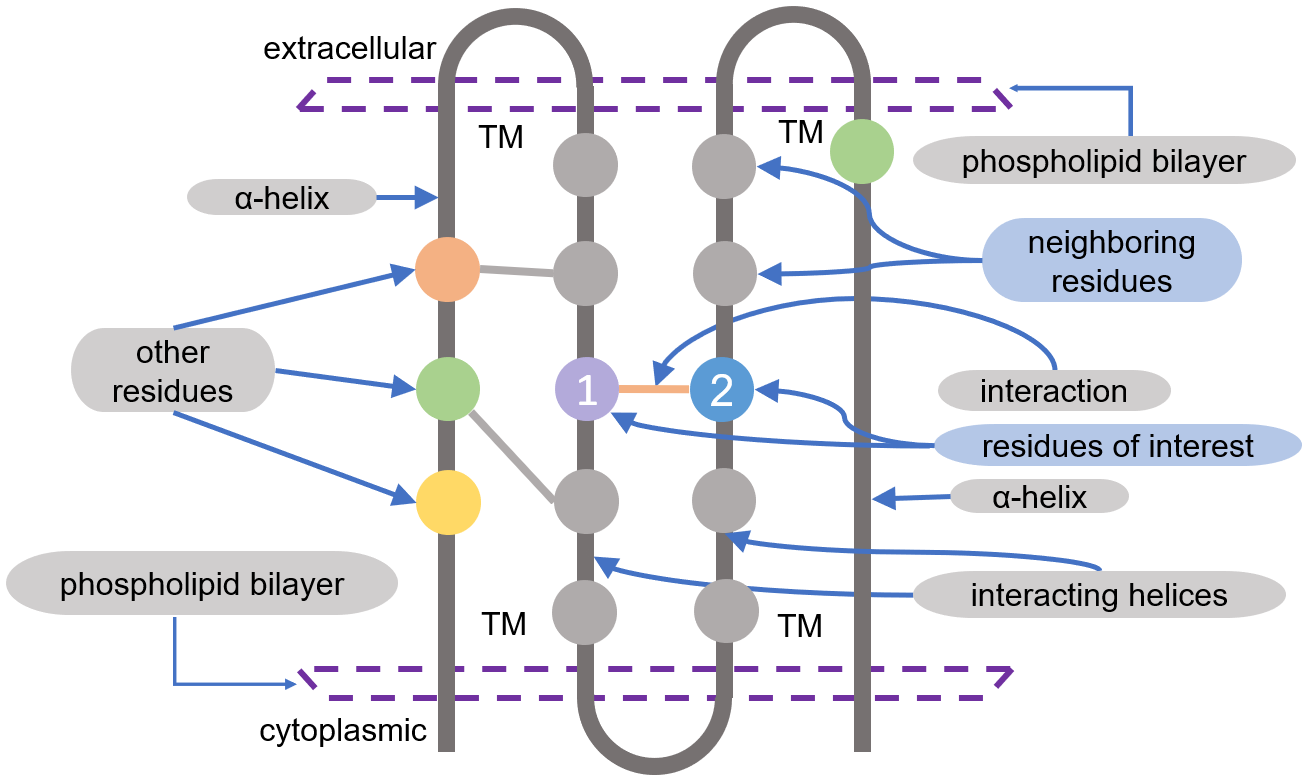
../../../_images/tmsc.png

Caption: Two residues facing each other in a pair of helices.#

Residue 1 and residue 2 connect to each other’s neighbouring residues, like below.

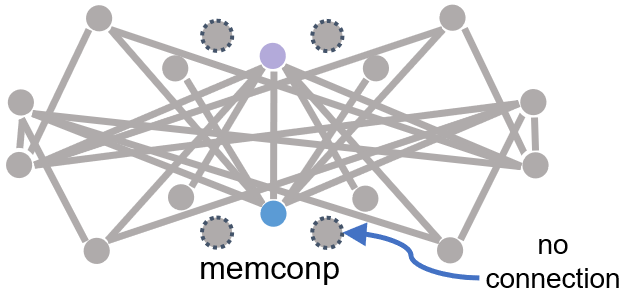
../../../_images/memconp.png

Caption: Helix-helix connections in MemConP in bipartite graphs.#

It is defined by a group of specified coordinates, like in the code area below.

bigraph = [
    [4, -4], [4, 4], [3, -4], [-4, 3], [3, 4],
    [4, 3], [0, -4], [0, 4], [0, -3], [0, 3],
    [-1, 0], [1, 0], [0, 0], [0, -1], [0, 1],
    [3, 0], [-3, 0], [4, 0], [-4, 0], [-3, -4],
    [-4, -3], [-3, 4], [4, -3], [-4, -4], [-4, 4],
]

Cross#

Next, residues can cross connected as cross as shown in the plot.

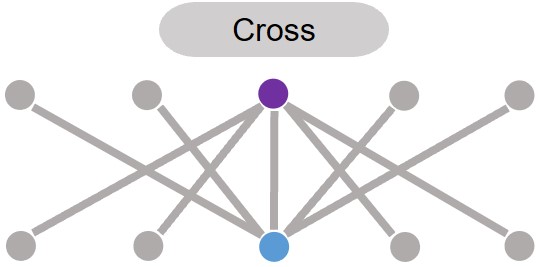
../../../_images/cross.jpg

Caption: Cross connections of two residues in a bipartite graph.#

We can represent this cross-style bigraph in Python, which can be recognized by TMKit.

bigraph = [
    [-1, 0], [1, 0], [0, 0], [0, 1], [0, -1],
]

Unchanged#

If we do not want to do anything with each residue pair, we can tell TMKit this way.

bigraph = [
    [0, 0],
]

Customized#

You can build your own bipartite graphs to obtain connections for testing! You can simply replace self.bigraph with coordinates you like.

self.bigraph = [
    ...
]
Contents